An Introduction to Basic Geometric Concepts for Students

Geometry is a fascinating branch of mathematics that deals with shapes, sizes, and the properties of space. It helps us understand the world around us better. From the simplest shapes we see daily to the complex structures in engineering and architecture, geometry is omnipresent. In this article, we will explore the fundamental geometric concepts that form the building blocks of this intriguing subject.

Points, Lines, and Planes

A point is a location in space with no size or dimension. Think of it as a dot on a piece of paper.

A line is a straight path that extends infinitely in both directions and has no thickness.

A line segment is a part of a line with a definite length that connects two distinct points.

A plane is a flat, two-dimensional surface that extends infinitely in all directions.

Types of Lines

In geometry, lines come in various types:

• Parallel Lines: These are lines that never meet and stay the same distance from each other at all times. Imagine the rails of a railway track.
• Perpendicular Lines: Lines that intersect at a right angle (90 degrees). Think of the corner of a book or a laptop.
• Intersecting Lines: Lines that cross each other at any angle.

Angles

Angles are formed when two lines or line segments meet at a point called the vertex. Angles are measured in degrees (°). Here are some common types of angles in mathematics:

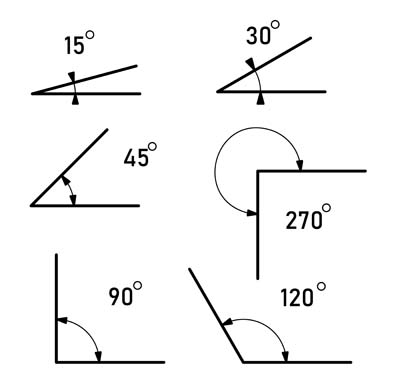
• Acute Angle: An angle less than 90°.
• Right Angle: This is an angle that measures exactly 90 degrees.
• Obtuse Angle: This type of angle is more than 90 degrees but less than 180 degrees.
• Straight Angle: An angle that measures exactly 180 degrees.

Triangles

Triangles are three-sided closed shapes and are classified based on their sides and angles.

• Equilateral Triangle: All three sides and angles are the same.
• Isosceles Triangle: Two sides and two angles are the same.
• Scalene Triangle: All sides and angles are unique.
• Right Triangle: One angle measures 90 degrees, making it a right angle.

Quadrilaterals

Quadrilaterals are four-sided closed shapes. These shapes are classified based on the length of their sides and the measure of their angles.

• Square: Every side and angle are the same, with each angle measuring 90°.
• Rectangle: The sides across from each other are equal, and all angles are 90°.
• Parallelogram: The sides that are opposite each other are both parallel and equal, but the angles can vary.
• Rhombus: All sides are the same length, but the angles can differ. The angles that are opposite each other are equal.
• Trapezoid: There is just one pair of parallel opposite sides.

Circle

A circle is a flat shape where all the points on its surface are equidistant from a fixed point called the centre. The radius is the distance from the centre of the circle to any point on its edge. There are some key components of a circle to know.

• Diameter: This is a line segment that goes through the centre and connects two points on the circle. Its length is double that of the radius.
• Circumference: The perimeter or boundary of the circle.
• Chord: A line segment connecting two points on the circle, but not necessarily passing through the centre.
• Arc: It is a part of the circumference of a circle.
• Sector: The region that is enclosed by two radii and an arc.

Polygons

Polygons are closed, two-dimensional shapes formed with 3 or more straight sides. Some of the common polygons —

• Pentagon: A five-sided polygon.
• Hexagon: A polygon with 6 sides.
• Octagon: An eight-sided polygon.

3D Shapes

Now let us enter the world of three-dimensional shapes of solids or polyhedra. Some common 3D shapes include:

• Cube: A solid with six equal square faces.
• Rectangular Prism: A solid with rectangular faces.
• Sphere: A perfectly round 3D shape, like a ball.
• Cylinder: A solid with two parallel circular bases and a curved surface connecting them.
• Cone: A solid with a circular base and a single vertex.
• Pyramid: A solid with a polygonal base and triangular faces that meet at a single point.

Table of Basic Geometric Concepts

Concept	Definition	Example
Point	A location in space with no size or dimension	A dot on a paper
Line	A straight path extending infinitely in both directions	The edge of a ruler
Plane	A flat, two-dimensional surface	A piece of paper
Angle	Formed when two lines meet at a point	Corners of a triangle
Triangle	Three-sided polygon	Pyramids, traffic signs
Quadrilateral	Four-sided polygon	Squares, rectangles
Circle	A set of points equidistant from the centre	Wheels, clock faces
Polygon	Closed shape with straight sides	Pentagons, hexagons
3D Shapes	Three-dimensional solids	Cubes, spheres, cylinders

Fascinating Facts

1. Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This theorem is named after the ancient Greek mathematician Pythagoras.

Hypotenuse² = (Side1)² + (Side2)²

2. Golden Ratio: This special number, approximately 1.618, appears in various natural and human-made structures, such as the spirals of seashells and the Parthenon in Greece.
3. Euler’s Formula: For polyhedra,

Euler’s formula states that,

 V – E + F = 2

where,

V is the number of vertices.

E is the number of edges.

 F is the number of faces.

This formula helps in understanding the properties of 3D shapes.

Conclusion

Geometry is an essential part of mathematics that helps us understand the shapes and structures of the world around us. From the simplest points and lines to complex three-dimensional shapes, geometric concepts form the foundation for many fields, including architecture, engineering, and art.

By exploring these basic geometric concepts, students can develop a deeper appreciation for the beauty and functionality of geometry in everyday life.

For more such informative/interesting blogs, visit Center Point School.